LD_clumping(连锁不平衡性聚类)

1.连锁不平衡性定义
连锁不平衡性(linkage disequilibrium)是指 不同基因座(loci)的等位基因(allele)之间非随机(nonrandom)的关联。
两个基因座互相独立不相关,即连锁平衡 linkage equilibrium 的状态。
常用的指标:D’, r2(相关系数,correlation coefficient)【更常用】
当D’=0,r2=0时,处于完全连锁平衡状态
当D’=1,r2=1时,处于完全连锁不平衡状态。
其中,从0-1之间的度量越高,LD越高,如果两个位点连锁,连锁程度也越高。
对应的连锁不平衡性越明显,说明对应位置的相关性就越强,他们就越可能在同一种表型中发挥相似的作用。
2.LD_clumping的定义
LD clumping(连锁不平衡修剪)是全基因组关联分析(GWAS)中常用的步骤,用于筛选与目标表型关联最强的独立SNP,同时移除与其高度连锁(即存在强LD)的冗余SNP。
算法原理:
- 索引SNP选择:
从GWAS结果中筛选p值小于--clump-p1的SNP,按p值升序排序作为候选索引SNP。(对应 的P值越小,证明其与对应的性状的相关性越强) - 区域修剪:
对每个索引SNP,在± --clump-kb范围内计算所有SNP的LD(r²)。若r2>–clump-r2,则移除该SNP,保留索引SNP作为代表。(如果这两个SNP之间的r2比较大,证明两者之间存在某种相关联性,保留p值比较小的SNP,删除掉对应的这个SNP) - 迭代过程:
从最显著SNP开始处理,完成后继续处理剩余SNP中最显著者,直至无满足条件的SNP。
生物学意义:
- 减少多重检验:通过去除冗余SNP降低假阳性
- 定位因果位点:保留独立信号,优先选择关联最强的SNP
- 提升可解释性:简化结果用于后续分析(如多基因风险评分)
注意事项:
- 参考群体匹配:参考基因型应与研究群体一致,否则LD估计偏差导致错误修剪2
- 参数敏感性:
- 宽松的r²阈值(如0.5)保留更多SNP
- 严格的p值阈值(如5e-8)减少假阳性
- 替代工具:
当参考数据缺失时,可用--clump-snp-field+--clump-p直接基于GWAS结果计算LD(精度较低)
3.LD_clumping代码命令
1 |
|
1 |
|
对应的运行启动sh文件的前提条件
1 | plinkFile="../04_Data_QC/sample_data.clean" |
对应的已经经过QC的完整的合理的数据的前缀后缀可为bed,bim,fam
1 | plink --bfile ${plinkFile}\ |
关键参数解析:
| 参数 | 说明 | 典型值 |
|---|---|---|
--clump-p1 |
索引SNP的最小显著性阈值(候选索引) | 5e-8 (全基因组显著) |
--clump-r2 |
连锁不平衡阈值(r² > 此值被移除) | 0.1~0.5 |
--clump-kb |
以索引SNP为中心的搜索范围 | 250~1000 kb |
--clump-field |
指定p值列名(若非常规列名) | P |
--out clumped_results |
对应的输出结果的前缀 | 略 |
输出文件
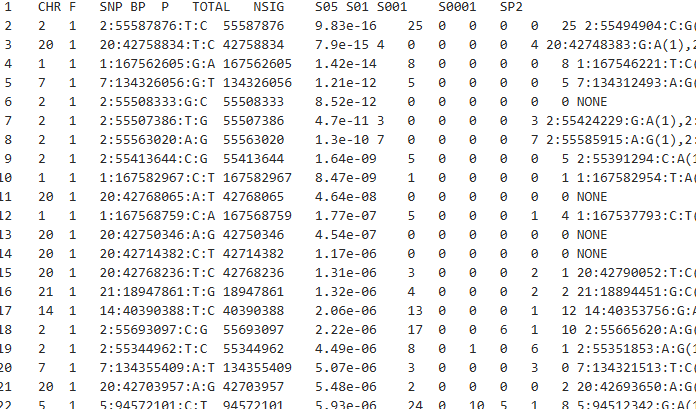
CHR:染色体编号
SNP:对应的SNP的唯一标识(主键)
BP:碱基突变的位置
P:对应的显著值
**TOTAL:**对应聚类中心所代表的聚类的SNP的数目
NSIG:clump中达到显著水平的SNP数(默认p<0.0001)
S05 S01 S001 S0001:p值小于0.05/0.01/0.001/0.0001的SNP数量
SP2:clump中与索引SNP相关性最强的次要SNP ID
后续列为其他次要SNP的ID
4.LD_clumping可视化
1 | import matplotlib.pyplot as plt |
1 |
|
1 | # 假设gwas_data是包含所有SNP的DataFrame,包含列:CHR, POS, P, SNP_ID |
1 | clumped |
| CHR | F | SNP | BP | P | TOTAL | NSIG | S05 | S01 | S001 | S0001 | SP2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 1 | 2:55587876:T:C | 55587876.0 | 9.830000e-16 | 25 | 0 | 0 | 0 | 0 | 25 2:55494904:C:G(1),2:55500529:A:G(1),2:55502... | NaN |
| 1 | 20 | 1 | 20:42758834:T:C | 42758834.0 | 7.900000e-15 | 4 | 0 | 0 | 0 | 0 | 4 20:42748383:G:A(1),20:42751035:T:C(1),20:427... | NaN |
| 2 | 1 | 1 | 1:167562605:G:A | 167562605.0 | 1.420000e-14 | 8 | 0 | 0 | 0 | 0 | 8 1:167546221:T:C(1),1:167548962:T:C(1),1:1675... | NaN |
| 3 | 7 | 1 | 7:134326056:G:T | 134326056.0 | 1.210000e-12 | 5 | 0 | 0 | 0 | 0 | 5 7:134312493:A:G(1),7:134355426:G:T(1),7:1343... | NaN |
| 4 | 2 | 1 | 2:55508333:G:C | 55508333.0 | 8.520000e-12 | 0 | 0 | 0 | 0 | 0 | 0 NONE | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 378810 | 11 | 1 | 11:95249340:T:C | 95249340.0 | 1.000000e+00 | 0 | 0 | 0 | 0 | 0 | 0 NONE | NaN |
| 378811 | 1 | 1 | 1:44123074:A:G | 44123074.0 | 1.000000e+00 | 0 | 0 | 0 | 0 | 0 | 0 NONE | NaN |
| 378812 | 8 | 1 | 8:87612144:C:T | 87612144.0 | 1.000000e+00 | 0 | 0 | 0 | 0 | 0 | 0 NONE | NaN |
| 378813 | 11 | 1 | 11:21582709:A:G | 21582709.0 | 1.000000e+00 | 0 | 0 | 0 | 0 | 0 | 0 NONE | NaN |
| 378814 | 14 | 1 | 14:67936045:A:G | 67936045.0 | 1.000000e+00 | 0 | 0 | 0 | 0 | 0 | 0 NONE | NaN |
378815 rows × 12 columns
1 | # 计算每个SNP的-log10(P) |
C:\Users\Administrator\AppData\Local\Temp\ipykernel_30944\2440510483.py:40: UserWarning: Creating legend with loc="best" can be slow with large amounts of data.
plt.tight_layout()
C:\Users\Administrator\AppData\Local\Temp\ipykernel_30944\2440510483.py:41: UserWarning: Creating legend with loc="best" can be slow with large amounts of data.
plt.savefig('LD_clumping.png')
d:\ProgramData\anaconda3\envs\py123\lib\site-packages\IPython\core\pylabtools.py:170: UserWarning: Creating legend with loc="best" can be slow with large amounts of data.
fig.canvas.print_figure(bytes_io, **kw)
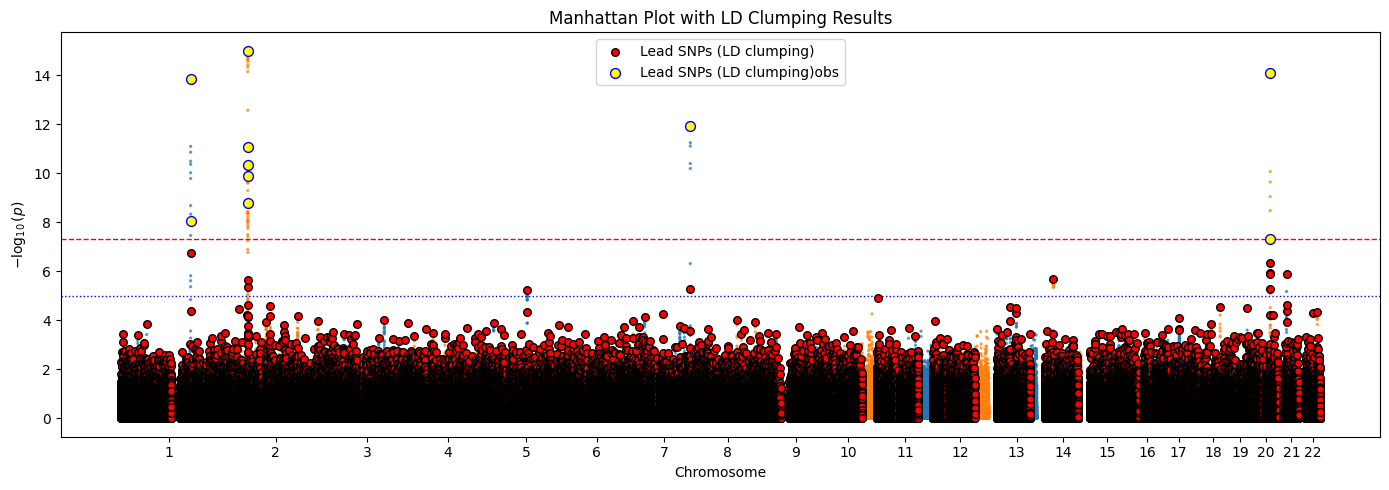
对应的黄色部分就是优先选择的索引点,但是聚类中心会不断进行迭代,最终的显著值会比较大
聚类结束可以看到聚类中心的显著值的-log10p大部分都处于图像的上层,这样的聚类中心具有价值。